Redis算法 HASH

发表于 | 分类于 | 阅读次数：

注:主要内容整理来自redis中几种哈希函数的研究
哈希就是离散算法
将一个键值转换成我们需要的数组索引下标的方法

哈希函数的准则

Thomas Wang认为的好的hash函数的特性

  • 一个好的哈希函数应该是可逆的。即，对于哈希函数输入值x和输出值y，如果存在f(x) = y，就一定存在g(y) = x。说白了，就是哈希函数可以将某一个值x转换成一个key，也可以把这个key还原回成x。
  • 一个好的哈希函数应该容易造成雪崩效应。这里的雪崩效应是从比特位的角度出发的，它指的是，输入值1bit位的变化会造成输出值1/2的bit位发生变化。

具有可逆性的哈希函数可以从根本上消除哈希过程中的冲突(collisions)。
但是因为存储空间有限,不可能完全没有冲突的存在,所以哈希函数应只负责将输入值尽量均匀的分布在某一空间，而不管实际的物理内存是否可以容纳该空间。
将这一问题留给具体的使用者。对于内存不足的情况，一般的处理方法是对哈希结果进行二次映射，将这些值存入到一个固定大小的物理内存块中。具体映射的方法有很多，最简单的是取余运算，但是取余的方法方法过于耗时，可以通过一个小技巧避免。我们可以将放置哈希结果的物理内存块的大小设置成2的n次方的形式，此时, tablesize = 2 ^n，key_addr =hash_value % tablesize = hash_value & (tablesize - 1)。这里用位运算来代替取余运算，在tablesize = 2 ^ n 的情况下，两者的效果相同。

雪崩效应的主要目的是使得哈希结果更为离散均匀。

可逆性

基本的可逆算法

  • x + 常数 = y；
  • x - 常数 = y；
  • x ^ 常数 = y；
  • ~x = y；
  • x * 常数 =y；
    在上面的式子中，我们可以通过x得到y，也可以通过y得到x，这没什么问题。

进阶的可逆问题

  • ( x + 常数 ) + ( x << n ) = y；是否可逆
    比如(x +(101111)2) + (x << 3) = (11101100)2
    可以转化为x + (x << 3) = (11101100)2- (101111)2= (10111101)2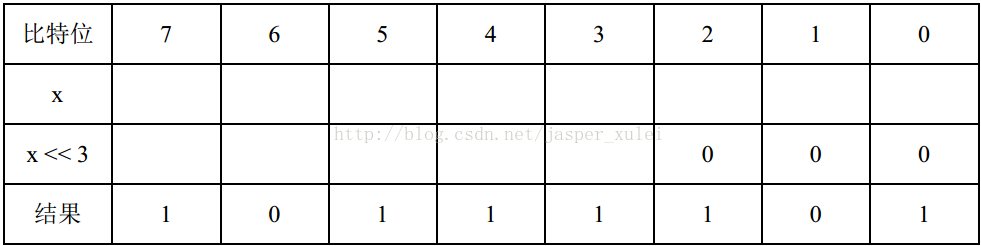 通过转换后的式子，我们可以画出这样一个表格，x + x<<3的最终结果为(10111101)2，而x<<3的最后三位为000，此时我们可以得到x的后三位为101，继而得到x<<3的后三位为相同101。如下图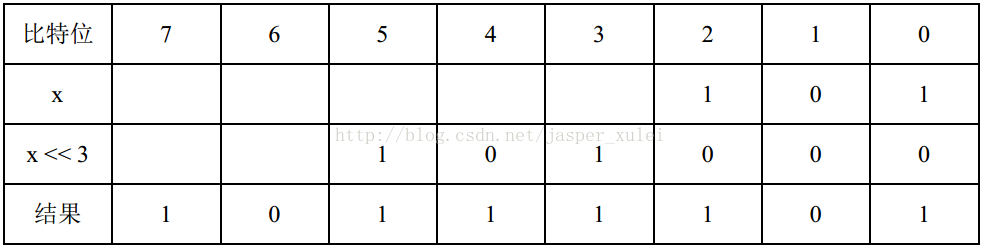： 此时，我们又可以得到x的第3、4、5位分别是0、1、0。依次类推，最终我们可以得到x=(10101)2，如下图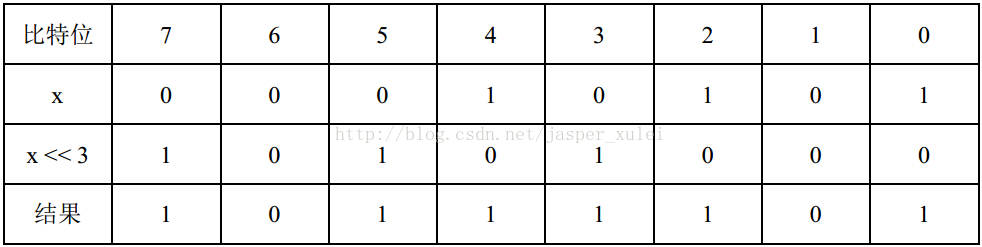： 所以，我们可以得知，式子1是可逆的。特别的，即使在位移过程中出现溢出截断，也不会影响结果。
  • ( x + 常数 ) + ( x >> n ) = y；是否可逆
    具体论证看引用的地址吧,不是很懂
    大概就是可逆的

雪崩效应

雪崩效应之前也讲过，说白了，就是输入数据1bit位的变化会导致输出数据N bit位的变化，这个N是大于等于1/2输出数据长度的。我们还是从简单的运算说起。

  • 加减运算
    加减运算很容易引起雪崩响应，这很容易理解，例如(1111)2+ (1)2 = (10000)2以及(1000)2 - (1)2 = (111)2这两个式子。
  • 位移运算
    取反运算也很容易产生雪崩效应，例如(00001111)2 << 2 = (00111100)2。
  • 乘除运算
    乘除运算的本质就是位移与加减法的组合，所以也是可以一起雪崩效应的。
  • 取反、异或运算
    取反和异或运算也很容易产生雪崩效应，如(1111)2~ =(0000)2以及(1101)2^ (1010)2=(0111)2。

Redis中的哈希算法的使用

32 bit MixFunction

就是左移右移等基本操作的组合

1
2
3
4
5
6
7
8
9
10
11
/* Thomas Wang's 32 bit Mix Function */
unsigned int dictIntHashFunction(unsigned int key)
{
    key += ~(key << 15);
    key ^=  (key >> 10);
    key +=  (key << 3);
    key ^=  (key >> 6);
    key += ~(key << 11);
    key ^=  (key >> 16);
    return key;
}

MurmurHash2

有MurmurHash1,MurmurHash2,MurmurHash3
redis中用的是MurmurHash2

将字符串视作int32进行hash运算
也都是最基础的算法
代码中的m,r的值为什么是这几个数字,只能说用这几个数字计算的结果效果好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
/* MurmurHash2, by Austin Appleby
 * Note - This code makes a few assumptions about how your machine behaves -
 * 1. We can read a 4-byte value from any address without crashing
 * 2. sizeof(int) == 4
 *
 * And it has a few limitations -
 *
 * 1. It will not work incrementally.
 * 2. It will not produce the same results on little-endian and big-endian
 *    machines.
 */
unsigned int dictGenHashFunction(const void *key, int len) {
    /* 'm' and 'r' are mixing constants generated offline.
     They're not really 'magic', they just happen to work well.  */
    uint32_t seed = dict_hash_function_seed;
    const uint32_t m = 0x5bd1e995;
    const int r = 24;

    /* Initialize the hash to a 'random' value */
    uint32_t h = seed ^ len;

    /* Mix 4 bytes at a time into the hash */
    const unsigned char *data = (const unsigned char *)key;

    while(len >= 4) {
        uint32_t k = *(uint32_t*)data;

        k *= m;
        k ^= k >> r;
        k *= m;

        h *= m;
        h ^= k;

        data += 4;
        len -= 4;
    }

    /* Handle the last few bytes of the input array  */
    switch(len) {
    case 3: h ^= data[2] << 16;
    case 2: h ^= data[1] << 8;
    case 1: h ^= data[0]; h *= m;
    };

    /* Do a few final mixes of the hash to ensure the last few
     * bytes are well-incorporated. */
    h ^= h >> 13;
    h *= m;
    h ^= h >> 15;

    return (unsigned int)h;
}

djb hash

不区分大小写的字符串hash算法

1
2
3
4
5
6
7
8
/* And a case insensitive hash function (based on djb hash) */
unsigned int dictGenCaseHashFunction(const unsigned char *buf, int len) {
    unsigned int hash = (unsigned int)dict_hash_function_seed;

    while (len--)
        hash = ((hash << 5) + hash) + (tolower(*buf++)); /* hash * 33 + c */
    return hash;
}